Abstract

In this work, an advanced novel small-scale non-orthogonal communication technique utilizing physical layer security (PLS) for enhanced security and reliability for two users is proposed. This work is motivated by current challenges faced by conventional non-orthogonal multiple access (NOMA) techniques, for instance, the recent exclusion of power-domain NOMA (PD-NOMA) from 3GPP release 17 due to its performance degradation resulting from channel estimation errors and the utilization of successive interference cancellation (SIC) algorithms at the receiver. The proposed model uses the wireless channel characteristics to eliminate user interference as well as completely degrade the received signal at the eavesdropper’s terminal. More specifically, auxiliary signals are precisely designed and superimposed on top of user signals from a dual-transmitter system to provide perfect secrecy against external and internal eavesdroppers, while providing low complexity at the receiver. The efficiency and novelty of the proposed system are presented via mathematical analysis and validated by Monte Carlo simulations. Results obtained indicate that the proposed model achieves less complex, secure, and more efficient communication, suitable for low power consumption and limited processing applications.

INDEX TERMS

Non-Orthogonal Multiple Access (NOMA), Security, 6G, Internet of Things, Wireless communication, Wireless security, Physical Layer Security.

Introduction

Internet of things (IoT) is a network of millions of interconnected wireless devices accessible through the internet [1]. The idea of IoT was made possible by advanced wireless communication technology (5G and beyond). This is due to the many advantages such as increased data rate, reduced delay, and enhanced cellular coverage in the communication technologies over preceding technologies [2]. These advantages will have a huge impact on future service delivery. Some areas influenced by IoT are autonomous driving, healthcare, entertainments, industrial appliances, smart cities, smart energy grids, sports, remote surgery, and drone delivery applications [3]. Therefore, countries around the world are employing IoT technologies to combat challenges such as traffic congestion, insecurity, and infrastructure management caused by overpopulation. The information shared by these devices is sensitive, hence, it is critical that the communication system used by IoT devices is secure in order to protect confidential information [1].
Due to its unique properties, non-orthogonal multiple access (NOMA) communication technique has received tremendous attention in the current 5G and future 6G technologies [4]. These properties include high spectral efficiency, low latency, improved coverage, and massive connectivity [4]. Nevertheless, NOMA has various security limitations that must be addressed. Firstly, an external eavesdropper can intercept messages between multiple NOMA users using the same resources simultaneously. Secondly, independent communication between legitimate NOMA users must be secured to prevent internal eavesdropping. Moreover, according to [5], power-domain NOMA is no longer considered as a work item in the 3rd generation partnership project (3GPP) and was excluded in release 17 due to numerous performance degradation issues. For example, it is common knowledge that power-domain NOMA systems utilizing successive interference cancellation (SIC) achieves higher connectivity and throughput than orthogonal multiple access (OMA) schemes [6], however, power-sharing among multiple NOMA users causes the degradation of signal-to-interference power Ratio (SINR) for each user.

Cryptography and Physical Layer Security (PLS) techniques are the two main security techniques used in current communication systems [4] [7] [8] such as NOMA. Nevertheless, according to [4], cryptographic methods are not enough to provide the required security in future communication paradigms due to the following reasons. Firstly, future networks will be made up of decentralized and diverse systems. Therefore, key sharing and management will be an extremely tedious and costly task. Secondly, future communication paradigms will include new technologies such as massive machine-type communications (mMTC) and ultra-reliable low-latency communications (URLLC). These systems are designed for low-power consumption and delay-sensitive applications. Therefore, application of cryptography-based methods on future communication systems will not be feasible. Thirdly, future communication paradigms will be applied to many different areas with varied levels of security. However, according to [9], encryption-based techniques can only provide binary-level security. Additionally, the emergence of supercomputers makes cryptography more vulnerable, as a security breach is just a matter of time [10].

On the other hand, PLS can explore the properties of the channel such as noise, channel randomness, and interference to utterly degrade the received signal at the illegitimate user’s terminal [9], hence achieving key-less secure transmission by signal design and signal processing techniques. In PLS, properly designed artificial noise (AN) is superimposed on legitimate users’ signal and hence eliminating the need for private key production and management, moreover, it facilitates flexible transmission through the design of adaptive communication protocol [1][11]. According to [9], PLS is a promising solution to the security threats faced by 5G and future 6G network devices.

There are numerous advantages of using PLS over conventional cryptography methods [9]. Firstly, PLS can utilize a commonly used channel between legitimate users to disrupt the received signal at the eavesdropper’s antenna. Hence eliminating the need to share and manage keys. Secondly, most PLS design techniques require simple signal processing methods. This is beneficial to services with limited processing and low power requirements [4]. Finally, according to [12], channel-dependent resource allocation and link adaptation schemes in PLS can be employed to design adaptive security models that are dependent on specific occurrences.

Numerous works in literature have proposed enhancing NOMA security using PLS designs and overcome NOMA security limitations. Authors in [13] propose a PLS design in cognitive radio inspired NOMA network with multiple primary and secondary users. The scheme pairs primary and secondary users according to their channel gain and then power-domain NOMA is used to transmit the signal. According to the authors, secrecy levels can be improved by pairing the primary users with the best channel gains or by reducing the number of secondary users. Additionally, authors in [14] propose a new secrecy beam-forming (SBF) scheme by exploiting the use of artificial noise to protect confidential information of two NOMA users. The paradigm is designed for multiple-input single-output non-orthogonal multiple access (MISO-NOMA) systems such that only the eavesdropper’s signal gets degraded. However, the proposed power-domain schemes still sufferers from SINR degradation.

Also, authors in [5] propose Waveform-Domain NOMA. The paradigm proposes the utilization of multiple waveforms in the same resource element (RE), where relevant waveforms are assigned to each user and then decoded at the receiver side. The drawback to this system is that it contains additional processing at the receiver. Which increases power consumption as well as complexity.

A reliable communication system for future wireless communication is expected to be safe and secure from all kinds of threats. There are two types of eavesdroppers that a communication paradigm must be secured against, external and internal eavesdroppers. An internal eavesdropper is a legitimate user who illegally acquires information from other users, while an external eavesdropper is not in the authorized users’ set. Moreover, an eavesdropper can be passive or active [4]. An active eavesdropper is one who has the channel state information (CSI) available at the receiver, while a passive eavesdropper does not have the CSI available at the receiver. Internal eavesdroppers are generally active while external are passive.

Based on the aforementioned discussion, the need for a new and robust NOMA technique utilizing PLS for enhanced security is recognized. This work proposes small-scale NOMA (SS-NOMA) paradigm, where, auxiliary signal superposition using time diversity is used to enhance communication security and reliability of future low-complexity, massive machine type communication. The main objectives and contribution of the proposed SS-NOMA design utilizing PLS are listed below.

Novelty and contributions of the proposed algorithm

The novelty and contributions of the proposed SS-NOMA paradigm are to develop a NOMA scheme with:

Low-power consumption.
PLS design against internal eavesdroppers
PLS design against external eavesdroppers.
Two rounds auxiliary-signal-base transmission for two users, which is more complex for eavesdropper decode private information compared to a single user.
Low complexity. Conventional NOMA systems use interference cancellation algorithms [4] such as successive interference cancellation (SIC) at the legitimate user’s receiver to cancel the interference. However, the proposed algorithm uses specially designed auxiliary signals to automatically cancel the interference. Hence simplifying transmission complexity.
Minimum computation. The channel matrices are diagonal, therefore, the inverse operation is simple. Consequently, the auxiliary signal matrices can be designed by simple computation.
No power-dependent communication for near and far NOMA users.

The remainder of this work is organized as follows: Section II provides a review on NOMA. Section III discusses the overall system model of the proposed system. The algorithm is discussed in detail in section IV. Section V talks about performance analysis. Section VI highlights the simulation results, and finally, the conclusion is presented in section VII.

A NOMA REVIEW

The evolution of multiple access schemes over the last few decades can clearly be observed as 1G, 2G, 3G, and 4G [15]. The respective corresponding multiple access technologies are frequency division multiple access (FDMA), time division multiple access (TDMA), code division multiple access (CDMA), and orthogonal frequency division multiple access (OFDMA) [16]. These multiple access communication technologies were designed for orthogonal multiple access (OMA) where wireless resources are orthogonally allocated to multiple users in time, frequency, and code domain, hence known as OMA communication techniques. Nevertheless, OMA is faced with a number of problems as enumerated below [15].

The number of supported users is limited to the number of available orthogonal resources.
Despite the different domain techniques (frequency, time, and code), the orthogonality is almost always destroyed by the effects of channel variations. Therefore, orthogonality restoration measures are implemented at the receiver leading to high complexity.

Hence, the challenge for OMA to support massive connectivity, which is a key requirement for 6G technologies persists. Additionally, OMA is unable to meet other critical requirements such as very high spectral efficiency and low latency [17]. NOMA was developed as a technique with the ability to support more users than available orthogonal resources and solve the problems of OMA. The novelty in the design of NOMA is to support non-orthogonal resource allocation but at the expense of increasing the complexity at the receiver where the non-orthogonal user’s signal is decoded.

A major milestone was achieved with NOMA technique when 3GPP LTE release 13 approved study item of downlink multi-user superposition technique (MUST) in an effort to standardize NOMA [6]. The main objectives of MUST according to [18][19][20][21][22][23][24] was:

To identify possible enhancements accomplished by downlink multiuser communication schemes in a single cell.
Investigate potential system-level gain and possible trade-offs between complexity and performance under real-world deployment conditions and traffic models.
Identify required standard changes needed to assist user equipment to cancel or suppress cell-to-cell interference.

The study item concluded that NOMA can increase system capacity and enhance user experience, where it is high performing during peak traffic load in the network, compared to sub-band scheduling case, it is more beneficial in user-perceived throughput for wideband scheduling, and also more beneficial in user-perceived throughput for cell-edge UEs compared to other UEs [6]. Additionally, LTE Release 14 has released a new work item of downlink MUST for LTE, with a central objective of developing necessary infrastructure to allow LTE to perform cell-to-cell multiuser superposition transmission for the physical downlink shared channel [23]. Moreover, multiple NOMA schemes have been investigated in literature[15][25][26], including power-domain NOMA (PD-NOMA) [27], sparse code multiple access (SCMA) [28], pattern division multiple access (PDMA) [29], resource spread multiple access (RSMA) [30], multi-user shared access (MUSA) [31], interleave-grid multiple access (IGMA) [32], Welch-bound equality spread multiple access (WSMA) [33], and interleave division multiple access (IDMA) [34].

The NOMA schemes mentioned above follow the superposition principle and can generally be placed under PD-NOMA or code-domain NOMA (CD-NOMA). However, since NOMA principle allows multiple user signals to be superimposed on the same resources, this leads to interference and security issues. In the subsequent sections, a novel NOMA inspired communication technique is modeled, the technique utilizes characteristics of the channel to provide perfect security to users as well as cancel interference without any additional processing at the receiver.

OVERALL SYSTEM MODEL

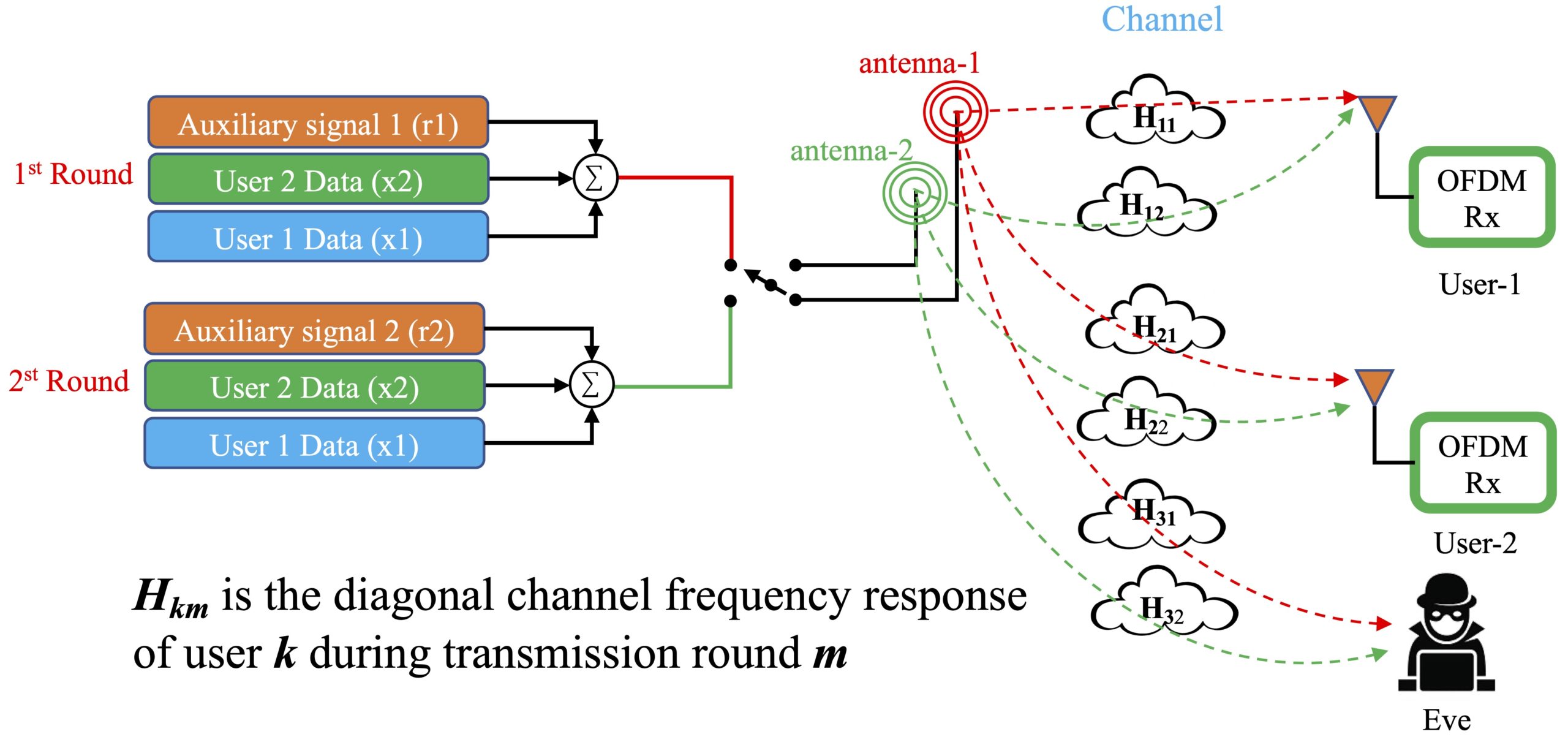
This communication technique can be modeled to serve any number of users. However, the scheme discussed in this work is designed for two users for simplicity purposes, where the system is composed of a dual-transmit antenna and two single-antenna legitimate users. The legitimate transmit antennas are trying to communicate with the users in the presence of a single-antenna eavesdropper as shown in Fig. 1. In addition, it is assumed that the transmitter has no knowledge of the passive eavesdropper’s channel. In the figure, the channel is indicated by $\mathbf{H_{km}}$ , which represents the diagonal channel frequency response of user $k$ during transmission round $m$ . The channels between $antenna-1$ and $antenna-2$ and all the users are assumed to be known at the transmitter and are taken to be slowly varying multi-path Rayleigh fading with the exponentially decaying channel.

Moreover, we employ channel sounding techniques to derive the channel from the transmitter to the receiver. The technique enables the reproduction of the channel using the receiver to transmitter channel in a time division duplexing (TDD) system. The proposed paradigm utilizes dual antennas for transmission, and the transmission is done in rounds. During each round, only one antenna is active, while the other is inactive. The active legitimate antenna wants to communicate to a particular user such that neither the external passive eavesdropper nor the internal active eavesdropper (other user) can decode the information.

FIGURE 1: Novel small scale NOMA multiple input single output OFDM detailed model.

PROPOSED ALGORITHMS

In this section, we focus on developing the proposed algorithm and justifying the calculations.

NOMA with auxiliary signal superposition

This work explores the use of auxiliary signals that are superimposed on user signals to enhance the security and reliability of future applications with limited processing abilities at the receiver [3]. The system is designed such that there are two transmissions from two different antennas. However, only one antenna is active during each transmission round. A superimposed auxiliary signal is calculated and added to the sum of the users’ signal during each transmission round. The downlink transmission from two different antennas is to ensure different channels. Consequently enabling the design of the auxiliary signals to guarantee secure and reliable communication against internal and external eavesdroppers. Moreover, communicating with two users during each transmission round make it very complex for the eavesdropper to decode the transmitted information. This is because the designed auxiliary signal is a function of both users’ channels. Compared to a single user system, a two-user system will provide perfect secrecy against eavesdroppers while making it easy for legitimate users to decode their respective signals.

The design of the proposed algorithm is as follows: A dual multi-carrier OFDM system with two transmit antennas is used, as shown in Fig. 2. Moreover, two single-antenna users and a passive eavesdropper are included in the system. The transmission process consists of two transmission rounds, where only one antenna is active during each transmission round as it can be observed from Fig. 1 (i.e., in round 1 $antenna-1$ is active $antenna-2$ is inactive, while in round 2 $antenna-2$ is active $antenna-1$ is inactive). Furthermore, it is assumed that both transmission rounds are within the coherence time of the channel. The frequency response of each OFDM symbol for user-1 and user- 2 at $antenna-1$ and $antenna-2$ can be represented as $\mathbf{x_1} = [x_0, x_1,..., x_{N_f-1}]$ and $\mathbf{x_2} = [x_0, x_1,..., x_{N_f-1}]$ respectively. Where $N_f$ is the total number of modulated symbols in one OFDM block, and both $\mathbf{x_1}$ and $\mathbf{x_1}$ $\in C^{[N_f \times 1]}$ .

Afterward, $\mathbf{x_1}$ and $\mathbf{x_2}$ are converted from serial to parallel and then their sum is added to the designed auxiliary matrix before transmission. The design steps of the auxiliary matrices for the proposed model are outlined in the subsequent discussion.

The signal from the first antenna after superposition to user-1 and user-2 is given as:

\begin{aligned} \mathbf{u_{1}}= \mathbf{x_{1}} + \mathbf{x_{2}} + \mathbf{r_{1}}. (1) \end{aligned}

Similarly, the signal from the second antenna is given as:

\begin{aligned} \mathbf{u_{2}}= \mathbf{x_{1}} + \mathbf{x_{2}} + \mathbf{r_{2}}, (2) \end{aligned}

where, $\mathbf{x_{1}}$ and $\mathbf{x_{2}}$ are the vector data in frequency domain for user-1 and user-2 respectively. Moreover, $\mathbf{r_{1}}$ and $\mathbf{r_{2}}$ are the auxiliary matrices expressly designed using the legitimate users’ channel. $\mathbf{r_{1}}$ and $\mathbf{r_{2}}$ will make sure that the signal received by user-1 and user-2 is secure from internal and external eavesdropping. In the following subsections, we will explain the details of the received signal at user-1, user-2, and eavesdropper. Afterward, we will explain the design of the auxiliary signals.

Received signal at User-1

The received signal in the frequency domain at user-1 during round-1 using $antenna-1$ can be given as:

\begin{aligned} \mathbf{y_{11}}= \mathbf{H_{11}}\mathbf{u_{1}} + \mathbf{z_{11}}, (3) \end{aligned}

where $\mathbf{H_{11}}$ is the frequency response of the channel and $\mathbf{z_{11}}$ is the additive white gaussian noise (AWGN) between user-1 and $antenna-1$ during round-1. Similarly, the received signal at user-1 during round-2 using $antenna-2$ is given as:

\begin{aligned} \mathbf{y_{12}}= \mathbf{H_{12}}\mathbf{u_{2}} + \mathbf{z_{12}}, (4) \end{aligned}

where $\mathbf{H_{12}}$ is the frequency response of the channel, and $\mathbf{z_{12}}$ is the AWGN between user-1 and $antenna-2$ during round-2. The combined received signal using maximum ratio combining (MRC) from round-1 and round-2 at user-1 can be written as:

\begin{aligned} \mathbf{\hat{y}_{1}}= \mathbf{H^H_{11}}\mathbf{y_{11}} + \mathbf{H^H_{12}}\mathbf{y_{12}}, (5) \end{aligned}

where $\mathbf{y_{11}}$ is the received signals at user-1 during round-1 through $antenna-1$ and $\mathbf{y_{12}}$ is the received signals at user-1 round-2 through antenna-2. $(\cdot)^H$ denotes the Hermitian transposition. After substituting the values of $\mathbf{y_{11}}$ and $\mathbf{y_{12}}$ in (5), the combined signal is written as follows:

\begin{aligned} \mathbf{\hat{y}_{1}}&=|\mathbf{H_{11}}|^2\mathbf{u_{1}} + \mathbf{H^H_{11}}\mathbf{z_{11}} + |\mathbf{H_{12}}|^2\mathbf{u_{2}} + \mathbf{H^H_{12}}\mathbf{z_{12}}, (6) \end{aligned}

where $\mathbf{u_{1}}$ and $\mathbf{u_{2}}$ are the superimposed transmitted signals during the first and second round. After substituting the values of $\mathbf{u_{1}}$ and $\mathbf{u_{2}}$ in (6), the combined signal is:

\begin{aligned} \mathbf{\hat{y}_{1}}&=|\mathbf{H_{11}}|^2(\mathbf{x_{1}} + \mathbf{x_{2}} + \mathbf{r_{1}}) + \mathbf{H^H_{11}}\mathbf{z_{11}} \\&\qquad\displaystyle + |\mathbf{H_{12}}|^2(\mathbf{x_{1}} + \mathbf{x_{2}} + \mathbf{r_{2}}) + \mathbf{H^H_{12}}\mathbf{z_{12}}. (7) \end{aligned}

Rearranging (7) and collecting like terms gives us:

\begin{aligned} \mathbf{\hat{y}_{1}}&=(|\mathbf{H_{11}}|^2 + |\mathbf{H_{12}}|^2)\mathbf{x_1} + (|\mathbf{H_{11}}|^2 + |\mathbf{H_{12}}|^2)\mathbf{x_2} \\&\qquad\displaystyle + |\mathbf{H_{11}}|^2 \mathbf{r_1} + |\mathbf{H_{12}}|^2\mathbf{r_2} + \mathbf{H^H_{11}}\mathbf{z_{11}} + \mathbf{H^H_{12}}\mathbf{z_{12}}. (8) \end{aligned}

The first term in (8) is the desired term with respect to user-1, while the remaining terms are undesired. The added auxiliary signals will ensure that the undesired terms, as well as the channel effects, are removed and canceled at user-1.

Received signal at User-2

Similar to user-1, the received signal in the frequency domain at user-2 during round-1 using $antenna-1$ is given as:

\begin{aligned} \mathbf{y_{21}}= \mathbf{H_{21}}\mathbf{u_{1}} + \mathbf{z_{21}}, (9) \end{aligned}

where $\mathbf{H_{21}}$ is the frequency response of the channel and $\mathbf{z_{21}}$ is the AWGN between user-2 and $antenna-1$ during round-1. Likewise, the received signal at user-2 during round-2 using $antenna-2$ is given as:

\begin{aligned} \mathbf{y_{22}}= \mathbf{H_{22}}\mathbf{u_{2}} + \mathbf{z_{22}}, %\nonumber (10) \end{aligned}

where $\mathbf{H_{22}}$ is the frequency response of the channel, and $\mathbf{z_{22}}$ is the AWGN between user-2 and $antenna-2$ during round-2. The combined received signal by using MRC from round-1 and round-2 at user-2 is:

\begin{aligned} \mathbf{\hat{y}_{2}}= \mathbf{H^H_{21}}\mathbf{y_{21}} + \mathbf{H^H_{22}}\mathbf{y_{22}}, (11) \end{aligned}

where $\mathbf{y_{21}}$ is the received signal at user-2 during round-1 from $antenna-1$ and $\mathbf{y_{22}}$ is the received signal at user-2 during round-2 from antenna-2. After substituting the values of $\mathbf{y_{21}}$ and $\mathbf{y_{22}}$ into (11), the combined signal is presented as follows:

\begin{aligned} \mathbf{\hat{y}_{2}}=|\mathbf{H_{21}}|^2\mathbf{u_{1}} + \mathbf{H^H_{21}}\mathbf{z_{21}} + |\mathbf{H_{22}}|^2\mathbf{u_{2}} + \mathbf{H^H_{22}}\mathbf{z_{22}}, (12) \end{aligned}

where $\mathbf{u_{1}}$ and $\mathbf{u_{2}}$ are the superimposed transmitted signals during the first and second round. Substituting the values of $\mathbf{u_{1}}$ and $\mathbf{u_{2}}$ into (12) results in the combined signal shown below.

\begin{aligned} \mathbf{\hat{y}_{2}}&=|\mathbf{H_{21}}|^2(\mathbf{x_{1}} + \mathbf{x_{2}} + \mathbf{r_{1}}) + \mathbf{H^H_{21}}\mathbf{z_{21}} \\&\qquad\displaystyle + |\mathbf{H_{22}}|^2(\mathbf{x_{1}} + \mathbf{x_{2}} + \mathbf{r_{2}}) + \mathbf{H^H_{22}}\mathbf{z_{22}}. (13) \end{aligned}

Rearranging (13) and collecting like terms gives us:

\begin{aligned} \mathbf{\hat{y}_{2}}&=(|\mathbf{H_{21}}|^2 + |\mathbf{H_{22}}|^2)\mathbf{x_1} + (|\mathbf{H_{21}}|^2 + |\mathbf{H_{22}}|^2)\mathbf{x_2} \\&\qquad\displaystyle + |\mathbf{H_{21}}|^2 \mathbf{r_1} + |\mathbf{H_{22}}|^2\mathbf{r_2} + \mathbf{H^H_{21}}\mathbf{z_{21}} + \mathbf{H^H_{22}}\mathbf{z_{22}}, (14) \end{aligned}

The second term in (14) is the desired term with respect to user-2 while the remaining terms are undesired. Likewise, the added auxiliary signals will make sure that the undesired terms, as well as the channel effects, are removed and canceled at user-2.

FIGURE 2. Dual multi-carrier OFDM system with two transmit antenna.

Received signal at Eavesdropper

For the case of the eavesdropper (Eve), the combined received signal from round-1 and round-2 is:

\begin{aligned} \mathbf{\hat{y}_{3}}= \mathbf{H^H_{31}}\mathbf{y_{31}} + \mathbf{H^H_{32}}\mathbf{y_{32}}, (15) \end{aligned}

where $\mathbf{y_{31}} = \mathbf{H_{31}}\mathbf{u_{1}} + \mathbf{z_{31}}$ and $\mathbf{y_{32}} = \mathbf{H_{32}}\mathbf{u_{2}} + \mathbf{z_{32}}$ are the received signal at the eavesdropper during round-1 and round-2 from $antenna-1$ and antenna-2, respectively, where $\mathbf{H_{31}}$ and $\mathbf{z_{31}}$ are the frequency response of the channel and AWGN between the eavesdropper and $antenna-1$ during round-1 while $\mathbf{H_{32}}$ and $\mathbf{z_{32}}$ are the frequency response of the channel and AWGN between the eavesdropper and $antenna-2$ during round-2. Substituting the values of $\mathbf{y_{31}}$ and $\mathbf{y_{32}}$ into (15) results in the following equation:

\begin{aligned} \mathbf{\hat{y}_{3}}=|\mathbf{H_{31}}|^2\mathbf{u_{1}} + \mathbf{H^H_{31}}\mathbf{z_{31}} + |\mathbf{H_{32}}|^2\mathbf{u_{2}} + \mathbf{H^H_{32}}\mathbf{z_{32}}, (16) \end{aligned}

\begin{aligned} \mathbf{\hat{y}_{3}}&=|\mathbf{H_{31}}|^2(\mathbf{x_{1}} + \mathbf{x_{2}} + \mathbf{r_{1}}) + \mathbf{H^H_{31}}\mathbf{z_{31}} \\&\qquad\displaystyle + |\mathbf{H_{32}}|^2(\mathbf{x_{1}} + \mathbf{x_{2}} + \mathbf{r_{2}}) + \mathbf{H^H_{32}}\mathbf{z_{32}}. (17) \end{aligned}

Rearranging (17) and collecting like terms gives us:

\begin{aligned} \mathbf{\hat{y}_{3}}&=(|\mathbf{H_{31}}|^2 + |\mathbf{H_{32}}|^2)\mathbf{x_1} + (|\mathbf{H_{31}}|^2 + |\mathbf{H_{32}}|^2)\mathbf{x_2} \\&\qquad\displaystyle + |\mathbf{H_{31}}|^2 \mathbf{r_1} + |\mathbf{H_{32}}|^2\mathbf{r_2} + \mathbf{H^H_{31}}\mathbf{z_{31}} + \mathbf{H^H_{32}}\mathbf{z_{32}}. (18) \end{aligned}

The eavesdropper will try to get information from both user-1 and user-2. Therefore, for Eve, both terms of equation (18) are desirable. However, as shown in (18) it is extremely difficult for Eve to cancel the interference it gets from users’ signals as well as that coming from auxiliary signals. Therefore, it is impossible for Eve to decode the signal for user-1 or user-2. The derivation of the values of the auxiliary signals, $\mathbf{r_1}$ and $\mathbf{r_2}$ , is explained in the subsequent section.

Designing the superimposed auxiliary signals for the proposed algorithm

In this section, we will design the auxiliary signals $\mathbf{r_1}$ and $\mathbf{r_2}$ such that the combined signal sent during round-1 and round-2 is received at the intended user with no extra computations at the receiver while providing meaningful and reliable information as well as protecting the user from internal and external eavesdroppers.

Auxiliary signals $\mathbf{r_1}$ and $\mathbf{r_2}$ are designed as follows: As illustrated in (8), the first term is the desired term for user-1. Therefore, the auxiliary signals $\mathbf{r_1}$ and $\mathbf{r_2}$ will be designed such that the effect of the channels on user-1 is removed as well as the interference by user-2 on user-1. Hence, the second, third, and fourth term in (8) should be equated to zero as follows:

\begin{aligned} (|\mathbf{H_{11}}|^2 + |\mathbf{H_{12}}|^2)\mathbf{x_2} + |\mathbf{H_{11}}|^2 \mathbf{r_1} + |\mathbf{H_{12}}|^2\mathbf{r_2} = 0. (19) \end{aligned}

Similarly, looking at (14), the second term of (14) is the desired term for user-2. Therefore, the auxiliary signals $\mathbf{r_1}$ and $\mathbf{r_2}$ will be designed such that the effect of the channels on user-2 is removed as well as the interference by user-1 on user-2. Hence, the first, third, and fourth term in (14) should be equal to zero and can be shown as:

\begin{aligned} (|\mathbf{H_{21}}|^2 + |\mathbf{H_{22}}|^2)\mathbf{x_1} + |\mathbf{H_{21}}|^2 \mathbf{r_1} + |\mathbf{H_{22}}|^2\mathbf{r_2} = 0. (20)\end{aligned}

Equations(19) and (20) can jointly be solved to determine the values of auxiliary signals $\mathbf{r_1}$ and $\mathbf{r_2}$ as follows:

\begin{aligned} \mathbf{r_{2}} = \frac{{(|\mathbf{H_{11}}|^2(|\mathbf{H_{21}}|^2 + |\mathbf{H_{22}}|^2)\mathbf{x_1} - |\mathbf{H_{21}}|^2 (|\mathbf{H_{11}}|^2 + }{|\mathbf{H_{12}}|^2)\mathbf{x_2}}}{|\mathbf{H_{12}}|^2|\mathbf{H_{21}}|^2 - |\mathbf{H_{11}}|^2|\mathbf{H_{22}}|^2}, (21)\end{aligned}

\begin{aligned} \mathbf{r_{1}} = \frac{-(|\mathbf{H_{21}}|^2 + |\mathbf{H_{22}}|^2)\mathbf{x_1} - |\mathbf{H_{22}}|^2\mathbf{r_{2}}}{|\mathbf{H_{21}}|^2}. (22) \end{aligned}

Using the auxiliary signals, $\mathbf{r_{1}}$ and $\mathbf{r_{2}}$ shown in (21) and (22), signals for user-1 and user-2 during round-1 and round-2 are send from the transmitters as shown in Fig.. The auxiliary signals will guarantee complete secrecy against internal and external eavesdroppers.

ALGORITHM’S PERFORMANCE ANALYSIS APPROACH

In this section, we will outline the approach used to analyze the performance of the system. We will start by discussing performance at the two legitimate users’ terminals (User-1 and User-2), then discuss the performance at the eavesdropper’s terminal.

Legitimate users (User-1, and User-2)

In order to conduct a performance analysis on the legitimate users, we will use numerical data fitting methods, similar to that used in [3]. To determine the BER at each legitimate user’s terminal, we must calculate the instantaneous signal-to-noise ratio $\gamma_b$ at each user’s node. The auxiliary signals $\mathbf{r_1}$ and $\mathbf{r_2}$ depicted in (21) and (22) respectively are designed to protect each user from inter-user interference as well as from the effects of the channel. According to [3], the distribution of the power of sub-channels corresponding to the received signal for each user must be determined so that $\gamma_b$ can be calculated using numerical data fitting method. Fig. 1 shows the power distribution of sub-channels corresponding to the received signal at the legitimate user. As it can be observed, the fitted distribution follows Weibull distribution with scale and shape parameters of $\omega= 1.53$ and $\mu=2.08$ respectively.

Analytical data fitting method proposed in [3] is used to compute the theoretical BER of the proposed NOMA schemes. The statistics of the effective instantaneous signal-to-noise ratio (SNR), $\gamma_b$ is first calculated for the legitimate user utilizing each scheme. The probability density function for the effective instantaneous SNR is calculated as:

\begin{aligned} P_{\gamma_b}\left(\gamma_b\right)\approx \left(\frac{1}{\omega}\right)^{\mu}\frac{1}{\Gamma \left(\mu\right)}\frac{\Omega^{\frac{3}{2}}\sqrt{\gamma_b}}{\hat{\gamma}^{\frac{3}{2}}_b}exp\left(-\frac{1}{\omega}\frac{\omega\gamma_b}{\hat{\gamma}_b}\right),(23) \end{aligned}

where $\Omega$ , $\hat{\gamma}_b$ , and $\Gamma \left(\mu\right)$ are the mean squire of the sub-channels, average SNR, and the gamma function respectively. $P_{\gamma_b}\left(\gamma_b\right)$ can then be used to calculate the BER.

\begin{aligned} BER_b=\frac{1}{2} \int_{0}^{\infty} erfc\left(\sqrt{\gamma_b}\right)P_{\gamma_b}\left(\gamma_b\right)d\gamma_b.(24)\end{aligned}

After substituting $P_{\gamma_b}\left(\gamma_b\right)$ in (24) with (24) we get the equation below:

\begin{aligned} BER_b=\frac{1}{2} \int_{0}^{\infty} erfc\left(\sqrt{\gamma_b}\right)\left(\frac{1}{\omega}\right)^{\mu}\frac{1}{\Gamma \left(\mu\right)}\frac{\Omega^{\frac{3}{2}}\sqrt{\gamma_b}}{\hat{\gamma}^{\frac{3}{2}}_b} exp\left(-\frac{1}{\omega}\frac{\omega\gamma_b}{\hat{\gamma}_b}\right)d\gamma_b. (25) \end{aligned}

According to [28] when (25) is simplified we get the equation below:

\begin{aligned} BER_b \approx \frac{\left(\frac{1}{\omega}\right)^{\mu}\frac{1}{\Gamma \left(\mu\right)}\frac{\Omega^{\frac{3}{2}}}{\hat{\gamma}^{\frac{3}{2}}_b}}{2\sqrt{\pi}}\left(\frac{arctan\left(\sqrt{\frac{1}{\omega}\frac{\omega}{\hat{\gamma}_b}}\right)}{2\frac{1}{\omega}\frac{\omega}{\hat{\gamma}_b}^{3/2}} - \frac{1}{2\frac{1}{\omega}\frac{\omega}{\hat{\gamma}_b}\left(1 + \frac{1}{\omega}\frac{\Omega}{\hat{\gamma}_b}\right)}\right), (26) \end{aligned}

where, $arctan\left(\cdot\right)$ denotes the inverse tangent.

FIGURE 3: Power distribution of sub-channels corresponding to the received signal at legitimate user (Bob)

Eavesdropper (Eve)

Analyzing the case for the eavesdropper, from equation (18) we observe that the eavesdropper is interested in information from both user-1 and user-2. The signal to interference at the eavesdropper’s terminal for listening to the signal deliberated for user-1 is given as:

\begin{aligned} SINR_{e1}&=\frac{(|\mathbf{H_{31}}|^2 + |\mathbf{H_{32}}|^2)\mathbf{|x_1|^2}} {(|\mathbf{H_{31}}|^2 + |\mathbf{H_{32}}|^2)\mathbf{|x_2|^2} + |\mathbf{H_{31}}|^2 \mathbf{r_1} + |\mathbf{H_{32}}|^2\mathbf{r_2} + \mathbf{\sigma^2_{31}} + \mathbf{\sigma^2_{32}}}, (27) \end{aligned}

where $\mathbf{\sigma^2_{31}}$ is the variance of channel noise corresponding to $\mathbf{H^H_{31}}\mathbf{z_{31}}$ and $\mathbf{\sigma^2_{32}}$ is the variance of channel noise corresponding to $\mathbf{H^H_{32}}\mathbf{z_{32}}$ . Likewise, The relevant signal to interference at the eavesdropper’s terminal for listening to the signal intended for user-2 is given as:

\begin{aligned} SINR_{e2}&=\frac{(|\mathbf{H_{31}}|^2 + |\mathbf{H_{32}}|^2)\mathbf{|x_2|^2}} {(|\mathbf{H_{31}}|^2 + |\mathbf{H_{32}}|^2)\mathbf{|x_1|^2} + |\mathbf{H_{31}}|^2 \mathbf{r_1} + |\mathbf{H_{32}}|^2\mathbf{r_2} + \mathbf{\sigma^2_{31}} + \mathbf{\sigma^2_{32}}} (28) \end{aligned}

Analyzing (27) and (28), we observe that there is tremendous inter-user interference depicted by the interference at the denominator of the equations. Additionally, $\mathbf{H_{11}}, \mathbf{H_{12}}, \mathbf{H_{21}}$ and $\mathbf{H_{22}}$ which are functions of $\mathbf{r_1}$ and $\mathbf{r_2}$ at the denominator are unknown to the eavesdropper. Consequently, this leads to severe degradation at the eavesdropper while trying to decode secured information intended for both user-1 and user-2.

SIMULATION RESULTS

In this section, we analyze the simulation results of the proposed algorithm using bit error rate (BER), throughput, and packet error rate as performance metrics. The parameters used in this work are depicted in the table below.

Table 1: system parameters used in the simulation setup of the proposed algorithm.

Channel	Multipath Rayleigh Fading Channel
Channel Length	9
Cyclic Prefix (CP)	9
FFT Size	64
Modulation Type	BPSK

The designed system uses OFDM transmitters $Tx_1$ and $Tx_2$ with 64 sub-carries for each user as shown in Fig. 2. In addition, a cyclic prefix (CP) of length 9 is used to prevent inter-symbol interference (ISI). The channel between the transmitters $Tx_1$ and $Tx_2$ , and receivers, user-1, user-2, and Eve, is assumed to be multi-path Rayleigh fading channel with equal number of taps $(L = 9)$ as shown in Table 1.

FIGURE 4: BER Vs SNR performance measure for the proposed algorithm.

Fig. 4 depicts the BER versus SNR graph for users utilizing the proposed algorithm, single input single output (SISO), and dual single input single output (SISO-dual) systems. From Fig. 4, it can be observed that the BER for both legitimate users labeled as user-1 and user-2 are similar. Moreover, the figure also shows the BER performance for internal and external eavesdroppers. Internal eavesdropping is when a legitimate user tries to illegally acquire information that is intended for the other user. For instance, when user-1 try to get information intended for user-2 (depicted as "user-1 listen To user-2") or when user-2 try to get information intended for user-1 (depicted as "user-2 listen To user-1"). It can be observed that the performance of both internal eavesdroppers is highly degraded. In addition, the figure also shows the BER performance of an external eavesdropper trying to eavesdrop on information intended for user-1 and user-2, labeled as "Eve listen To user-1" and "Eve listen To user-2" respectively. Similarly, we observe tremendous BER degradation due to (27) and (28).

Fig. 4 also shows the BER performance of two distinct transmission mechanisms, where users are utilizing SISO with dual transmission (SISO-dual), and users utilizing SISO with single transmission. It can be observed that SISO-dual has better BER performance than SISO. Hence, the proposed system is implemented using dual transmission. Moreover, It can also be observed that users employing SISO-dual have better BER performance compared to the proposed algorithm. Nevertheless, it does not provide secure communication as the proposed scheme.

FIGURE 5: Throughput performance measure for the proposed algorithm in comparison with dual-SISO and SISO systems.

Fig. 5 shows the throughput analysis for users utilizing the proposed algorithm, SISO, and SISO-dual systems. From Fig. 5, we can observe that the throughput performance for a SISO system performs better than an SISO-dual system. Nevertheless, the independent throughput performance of user-1 and user-2 outperforms the throughput performance for SISO. Moreover, it can be observed from the figure that the throughput performance of the external eavesdropper trying to obtain information intended for user-1 (Eve listen To user-1) and user-2 (Eve listen To user-2) is very degraded.

FIGURE 6: Packet error rate of the proposed algorithm.

Fig. 6 shows the packet error rate (PER) of the proposed algorithm. From the figure, it can be observed that the PER for both user-1 and user-2 are similar and better than the PER of the eavesdropper. The PER of the eavesdropper trying to eavesdrop on the information of user-1 (Eve listen To user-1) and user-2 (Eve listen To user-2) are 1. This further demonstrates the security of the proposed system attained by utilizing auxiliary superimposed signals obtained by exploiting the characteristics of the channel as shown in (21) and (22).

FIGURE 7: Peak to Average Power Ratio (PAPR) of the proposed algorithm.

Fig. 7 depicts the peak to average power ratio (PAPR) of a conventional OFDM system and an OFDM system utilizing the proposed algorithm. Tx1-proposed and Tx2-proposed are the PAPR of the first and second antenna using the proposed NOMA technique, while Tx1-conventional and Tx2-conventional are the PAPR of the first and second antenna using a conventional OFDM system. Fig. 7 clearly indicates that users utilizing the proposed algorithm have better PAPR performance than these using conventional OFDM. Hence, the proposed system solves one major problem experienced by OFDM systems [35], by reducing the PAPR leading to better spectral and energy efficiency.

FIGURE 8: Robustness of the proposed algorithm under imperfect channel conditions.

Finally, it is critical to analyze the robustness of the proposed PLS algorithm to an imperfect channel. Therefore, a channel error $\mathbf{\Delta h}$ is injected into the actual channel $\mathbf{H}_{ij}$ based on the values of MSE of a least-square estimator, where $i$ and $j$ are the user number and transmission round respectively, and $i \leq 3$ and $j \leq 2$ . The imperfect channel is given as: $\mathbf{\hat{H}}_{ij} = \mathbf{H}_{ij} + \mathbf{\Delta h}$ [36]. $\mathbf{H_{ij}}$ was used to calculate the auxiliary signals as shown in (21) and (22), but the signal is transmitted through $\mathbf{\hat{H}_{ij}}$ which is not a similar channel since $\mathbf{\Delta h}$ was added. $\mathbf{\Delta h}$ can be modeled as an independent AWGN with zero mean and variance $\sigma^2$ , where $\sigma^2 = e \times 10^{\frac{-SNR_{dB}}{10}}$ . $e$ is used to measure the quality of the estimator, the lower the value of $e$ , the higher the quality of the estimator. Hence Fig. 8 is drawn to measure the robustness of the proposed system.

Fig. 8 depicts the BER versus SNR plot of the proposed paradigm under different qualities of the estimator, that is, $e$ equals to 0, 0.05, 0.2, and 1. Moreover, the figure also shows the BER performance of near and far users utilizing conventional NOMA. It can be observed that there is a slight BER performance degradation as the quality of the estimator degrades. Nevertheless, there is a vast number of algorithms in literature used to enhance the performance of the estimator [36]. Also, it can be enhanced either by increasing the power of the training sequence or by using a pilot with a longer length. Nevertheless, the BER performance of the proposed design with an imperfect channel still outperforms the BER performance of convention NOMA users as can be observed from Fig. 8.

CONCLUSION

This work proposes the design of a secure, resilient, effective, and low complexity NOMA communication scheme that can provide zero information leakage to both external and internal eavesdroppers (perfect secrecy) without having the receiver to do any additional processing. The scheme is made up of two transmitters, and transmission is carried out during two transmission rounds. Two distinct channel-dependent auxiliary signals are added to the sum of the transmitted signals of user-1 and user-2, one auxiliary signal during each transmission round such that each legitimate user gets their intended signal after the two transmission rounds, while the eavesdropper gets the much-degraded version of the signal. The paradigm is validated with mathematical models and simulations. The obtained results demonstrate that the proposed system is able to provide reliable and secure communication with minimum complexity than conventional communication techniques. Hence making the proposed model suitable for IoT applications with low complexity and low power requirements. In the future, we intend to model this communication technique with more than two users.

Simulation codes

The simulation codes used to generate the results presented in this paper can be found at this link.

Authors Bio.

Jehad M. Hamamreh received the B.Sc. degree in electrical and telecommunication engineering from An-Najah University, Nablus, in 2013, and the Ph.D. degree in electrical-electronics engineering and cyber systems from Istanbul Medipol University, Turkey, in 2018. He was a Researcher with the Department of Electrical and Computer Engineering at Texas A and M University. He is currently an Assistant Professor with the Electrical and Electronics Engineering Department, Antalya International (Bilim) University, Turkey. https://sites.google.com/view/wislab/

His current research interests include wireless physical and MAC layers security, orthogonal frequency-division multiplexing multiple-input multiple-output systems, advanced waveforms design, multi-dimensional modulation techniques, IoT, 5G & 6G and orthogonal/non-orthogonal multiple access schemes for future wireless systems. He is serve as an Editor and a Regular Referee for various journals as well as a TPC Member for several international conferences.

Joel P. Lemayian received the B.Sc. degree in electrical and electronics engineering from Middle East Technical University Turkey, in 2017. He is presently pursuing the master’s (M.Sc.) degree in electrical and computer engineering. He is currently with Antalya Bilim University, Turkey.

He has worked as a research assistant in both Middle East Technical University and Antalya Bilim University in Internet of Things (IoT) lab and Neuroscience lab respectively. He is an author of numerous journals, conference papers and book chapters. His research interests include physical layer security, 5G Communication networks, Artificial Intelligence, Machine Learning, and IoT and its applications.

A Novel Small-Scale Nonorthogonal Communication Technique Using Auxiliary Signal Superposition with Enhanced Security for Future Wireless Networks